Mathematical aspects of analysis of maximal pressure-volume work function

Abstract

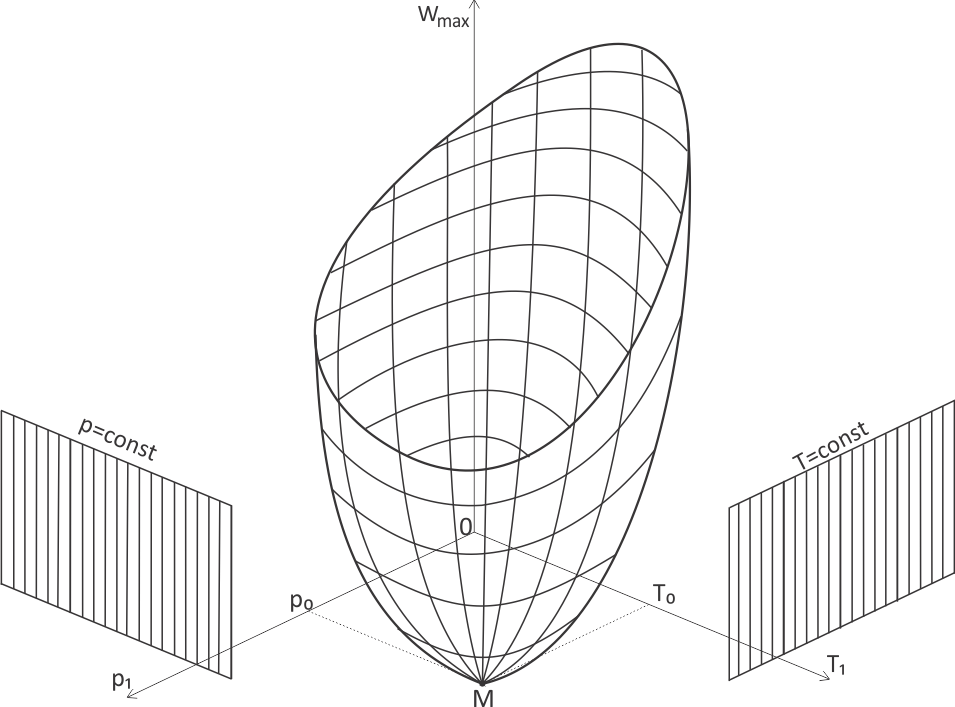
The paper presents relation for maximal pressure-volume work for closed systems by using principles of I and II law of thermodynamics, used in reversible processes in which mechanical and thermal balance has been achieved. For full interpretation of this problem for two characteristic cases, graphical review in p-v diagram is given, where in an obvious way is noticed that maximal expansion work is composed of isentropic and isothermal work as well as work against pressure of environment. On basis of derived relation, by using appropriate thermodynamic relations, expression for specific maximal work is obtained which is suitable for the analysis. That expression was observed like two-dimensional problem i.e. as function of two variables: initial pressure and initial temperature as primary parameters. Using mathematical analysis is proven existence of minimum of this function, function as well as its graphical presentation in three-dimensional coordinate system. Detailed mathematical analysis is presented that in general case function of maximal geometric work is one concave area in space. For efficient solving and analysis of this problem, complex function of maximal work is observed as two functions with one variable i.e. from two-dimensional problem we will make two single-dimensional problems. It’s proven that in single-dimensional problems also exists point in which maximal work is minimal and different from zero. At the end of the paper, opportunities for usage of this complex issues of maximal work which refer to exergy analysis and optimization of thermodynamic processes, also the guidelines for future research for problems of other gases, half – ideal gases and Van der Waals’s gas. It can be claimed that the procedure of analyzing thermodynamic function of maximal work, showed in paper, isn’t common in literature.